2.2 Bisection method#
Let’s recall the Intermediate Value Theorem (IVT), Theorem 4: If a continuous function \(f\) defined on \([a,b]\) satisfies \(f(a)f(b)<0,\) then there exists \(p\in[a,b]\) such that \(f(p)=0.\)
Here is the idea behind the method. At each iteration, divide the interval \([a,b]\) into two subintervals and evaluate \(f\) at the midpoint. Discard the subinterval that does not contain the root and continue with the other interval.
Example 13
Compute the first three iterations by hand for the function plotted in Figure 2.
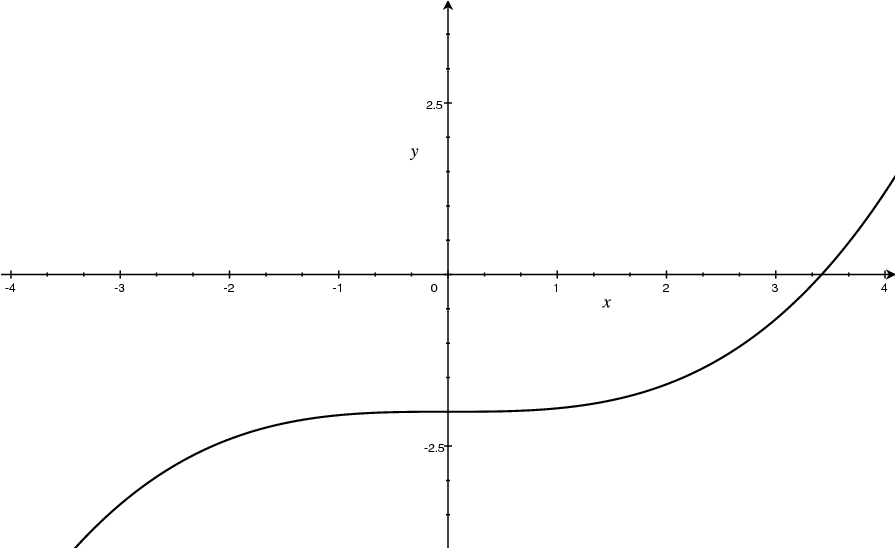
Fig. 2 .#
Step 1: To start, we need to pick an interval \([a,b]\) that contains the root, that is, \(f(a)f(b)<0\). From the plot, it is clear that \([0,4]\) is a possible choice. In the next few steps, we will be working with a sequence of intervals. For convenience, let’s label them as \([a,b]=[a_1,b_1],[a_2,b_2],[a_3,b_3],\) etc. Our first interval is then \([a_1,b_1]=[0,4]\). Next we find the midpoint of the interval, \(p_1=4/2=2,\) and use it to obtain two subintervals \([0,2]\) and \([2,4]\). Only one of them contains the root, and that is \([2,4]\).
Step 2: From the previous step, our current interval is \([a_2,b_2]=[2,4]\). We find the midpoint1 \(p_2=\frac{2+4}{2}=3\), and form the subintervals \([2,3],[3,4]\). The one that contains the root is \([3,4]\).
Step 3: We have \([a_3,b_3]=[3,4]\). The midpoint is \(p_3=3.5\). We are now pretty close to the root visually, and we stop the calculations!
In this simple example, we did not consider
Stopping criteria
It’s possible that the stopping criterion is not satisfied in a reasonable amount of time. We need a maximum number of iterations we are willing to run the code with.
Remark 3
A numerically more stable formula to compute the midpoint is \(a+\frac{b-a}{2}\) (see Example 8).
There is a convenient stopping criterion for the bisection method that was not mentioned before. One can stop when the interval \([a,b]\) at step \(n\) is such that \(|a-b|<\epsilon\). This is similar to the first stopping criterion discussed earlier, but not the same. One can also use more than one stopping criterion; an example is in the Python code that follows.
Python code for the bisection method#
In Example 13, we kept track of the intervals and midpoints obtained from the bisection method, by labeling them as \([a_1,b_1],[a_2,b_2],...,\) and \(p_1,p_2,...\). So at step \(n\) of the method, we know we are working on the interval \([a_n, b_n]\) and its midpoint is \(p_n\). This approach will be useful when we study the convergence of the method in the next theorem. However, keeping track of the intervals and midpoints is not needed in the computer code. Instead, in the Python code below, we will let \([a,b]\) be the current interval we are working on, and when we obtain a new interval in the following step, we will simply call the new interval \([a,b]\), overwriting the old one. Similarly, we will call the midpoint \(p\), and update it at each step.
import numpy as np
def bisection(f, a, b, eps, N):
"""
Perform the bisection method
input:
f: function, the function f
a, b: float, the left and right ends
eps: float, the tolerance; once (b-a)<eps, stop
N: int, the maximum number of steps to run the algorithm
"""
n = 1
p = 0. # to ensure the value of p carries out of the while loop
while n <= N:
p = a + (b-a)/2
if np.isclose(f(p), 0) or np.abs(a-b)<eps:
print('p is ', p, ' and the iteration number is ', n)
return
if f(a)*f(p) < 0:
b = p
else:
a = p
n += 1
y = f(p)
print('Method did not converge. The last iteration gives ',
p, ' with function value ', y)
Let’s use the bisection method to find the root of \(f(x)=x^5+2x^3-5x-2\), with \(\epsilon=10^{-4}\). Note that \([0,2]\) contains a root, since \(f(0)<0\) and \(f(2)>0\). We set \(N=20\) below.
bisection(lambda x: x**5+2*x**3-5*x-2, 0, 2, 1e-4, 20)
p is 1.319671630859375 and the iteration number is 16
The value of the function at the estimated root is:
x = 1.319671630859375
x**5+2*x**3-5*x-2
0.000627945623044468
Let’s see what happens if (N) is set too small and the method does not converge.
bisection(lambda x: x**5+2*x**3-5*x-2, 0, 2, 1e-4, 5)
Method did not converge. The last iteration gives 1.3125 with function value -0.14562511444091797
Theorem 6
Suppose that \(f\in C^0[a,b]\) and \(f(a)f(b)<0\). The bisection method generates a sequence \(\{p_{n}\}\) approximating a zero \(p\) of \(f(x)\) with
Proof. Let the sequences \(\{a_{n}\}\) and \(\{b_{n}\}\) denote the left-end and right-end points of the subintervals generated by the bisection method. Since at each step the interval is halved, we have
By mathematical induction, we get
Therefore \(b_{n}-a_{n}=\frac{1}{2^{n-1}}(b-a).\) Observe that
and thus \(|p_{n}-p|\rightarrow0\) as \(n\rightarrow\infty\).
Corollary 1
The bisection method has linear convergence.
Proof. The bisection method does not satisfy (3) for any \(C<1\), but it satisfies a variant of (4) with \(C=1/2\) from the previous theorem.
Finding the number of iterations to obtain a specified accuracy: Can we find \(n\) that will ensure \(|p_{n}-p|\leq10^{-L}\) for some given \(L\)?
We have, from the proof of the previous theorem (see (5)) : \(|p_{n}-p|\leq \frac{1}{2^{n}}(b-a)\). Therefore, we can make \(|p_{n}-p|\leq10^{-L}\), by choosing \(n\) large enough so that the upper bound \(\frac{1}{2^{n}}(b-a)\) is less than \(10^{-L}:\)
Example 14
Determine the number of iterations necessary to solve \(f(x)=x^5+2x^{3}-5x-2=0\) with accuracy \(10^{-4},a=0,b=2\).
Solution.
Since \(n\geq\log_{2}\left(\frac{2}{10^{-4}}\right)=4\log_{2}10+1=14.3\), the number of required iterations is 15.
Exercise 2.2-1
Find the root of \(f(x)=x^{3}+4x^{2}-10\) using the bisection method, with the following specifications:
a. Modify the Python code for the bisection method so that the only stopping criterion is whether \(f(p)=0\) (remove the other criterion from the code). Also, add a print statement to the code, so that every time a new \(p\) is computed, Python prints the value of \(p\) and the iteration number.
b. Find the number of iterations \(N\) necessary to obtain an accuracy of \(10^{-4}\) for the root, using the theoretical results of Section 2.2 Bisection method. (The function \(f(x)\) has one real root in \((1,2)\), so set \(a=1,b=2\).)
c. Run the code using the value for \(N\) obtained in part (b) to compute \(p_{1},p_{2},...,p_{N}\) (set \(a=1,b=2\) in the modified Python code).
d. The actual root, correct to six digits, is \(p=1.36523\). Find the absolute error when \(p_N\) is used to approximate the actual root, that is, find \(|p-p_N|\). Compare this error, with the upper bound for the error used in part (b).
Exercise 2.2-2
Find an approximation to \(25^{1/3}\) correct to within \(10^{-5}\) using the bisection algorithm, following the steps below:
a. First express the problem as \(f(x)=0\) with \(p=25^{1/3}\) the root.
b. Find an interval \((a,b)\) that contains the root, using Intermediate Value Theorem.
c. Determine, analytically, the number of iterations necessary to obtain the accuracy of \(10^{-5}\).
d. Use the Python code for the bisection method to compute the iterate from (c), and compare the actual absolute error with \(10^{-5}\).
- 1
Notice how we label the midpoints, as well as the endpoints of the interval, with the step number.
