2.6 Fixed-point iteration#

Many root-finding methods are based on the so-called fixed-point iteration, a method we discuss in this section.

Definition 6

A number \(p\) is a fixed-point for a function \(g(x)\) if \(g(p)=p.\)

We have two problems that are related to each other:

  • Fixed-point problem: Find \(p\) such that \(g(p)=p.\)

  • Root-finding problem: Find \(p\) such that \(f(p)=0.\)

We can formulate a root-finding problem as a fixed-point problem, and vice versa. For example, assume we want to solve the root finding problem, \(f(p)=0.\) Define \(g(x)=x-f(x),\) and observe that if \(p\) is a fixed-point of \(g(x)\), that is, \(g(p)=p-f(p)=p,\) then \(p\) is a root of \(f(x)\). Here the function \(g\) is not unique: there are many ways one can represent the root-finding problem \(f(p)=0\) as a fixed-point problem, and as we will learn later, not all will be useful to us in developing fixed-point iteration algorithms.

The next theorem answers the following questions: When does a function \(g\) have a fixed-point? If it has a fixed-point, is it unique?

Theorem 9

  1. If \(g\) is a continuous function on \([a,b]\) and \(g(x)\in[a,b]\) for all \(x\in[a,b]\), then \(g\) has at least one fixed-point in \([a,b]\).

  2. If, in addition, \(|g(x)-g(y)|\leq\lambda|x-y|\) for all \(x,y\in[a,b]\) where \(0<\lambda<1,\) then the fixed-point is unique.

Proof. Consider \(f(x)=g(x)-x\). Assume \(g(a)\neq a\) and \(g(b)\neq b\) (otherwise the proof is over.) Then \(f(a)=g(a)-a>0\) since \(g(a)\) must be greater than \(a\) if it’s not equal to \(a\). Similarly, \(f(b)=g(b)-b<0\). Then from IVT, there exists \(p\in(a,b)\) such that \(f(p)=0\), or \(g(p)=p\). To prove part 2, suppose there are two different fixed-points \(p,q\). Then

\[\begin{equation*} |p-q|=|g(p)-g(q)|\leq\lambda|p-q|<|p-q| \end{equation*}\]

which is a contradiction.

Remark 6

Let \(g\) be a differentiable function on \([a,b]\) such that \(|g'(x)|\leq k\) for all \(x\in(a,b)\) for some positive constant \(k<1\). Then the hypothesis of part 2 of Theorem 9 is satisfied with \(\lambda=k.\) Indeed, from the mean value theorem

\[\begin{equation*} |g(x)-g(y)|=|g'(\xi)(x-y)|\leq k|x-y| \end{equation*}\]

for all \(x,y\in[a,b].\)

The following theorem describes how we can find a fixed point.

Theorem 10

If \(g\) is a continuous function on \([a,b]\) satisfying the conditions

  1. \(g(x)\in[a,b]\) for all \(x\in[a,b]\),

  2. \(|g(x)-g(y)|\leq\lambda|x-y|\), for \(x,y\in[a,b]\) where \(0<\lambda<1,\) then the fixed-point iteration

\[\begin{equation*} p_{n}=g(p_{n-1}),n\geq1 \end{equation*}\]

converges to \(p,\) the unique fixed-point of \(g\) in \([a,b]\), for any starting point \(p_{0}\in[a,b]\).

Proof. Since \(p_{0}\in[a,b]\) and \(g(x)\in[a,b]\) for all \(x\in[a,b]\), all iterates \(p_{n}\in[a,b]\). Observe that

\[\begin{equation*} |p-p_{n}|=|g(p)-g(p_{n-1})|\leq\lambda|p-p_{n-1}|. \end{equation*}\]

Then by induction, \(|p-p_{n}|\leq\lambda^{n}|p-p_{0}|\). Since \(0<\lambda<1\), \(\lambda^{n}\rightarrow0\) as \(n\rightarrow\infty\), and thus \(p_{n}\rightarrow p\).

Remark 7

Theorem 10 still holds if the second condition \(|g(x)-g(y)|\leq\lambda|x-y|\), is replaced by \(|g'(x)|\leq k\) for all \(x\in[a,b]\) where \(0<k<1\). (See Remark 6).

Corollary 3

If \(g\) satisfies the hypothesis of Theorem 10, then the following error bounds hold.

  1. \(|p-p_{n}|\leq\frac{\lambda^{n}}{1-\lambda}|p_{1}-p_{0}|\)

  2. \(|p-p_{n}|\leq\frac{1}{1-\lambda}|p_{n+1}-p_{n}|\)

  3. \(|p-p_{n+1}|\leq\frac{\lambda}{1-\lambda}|p_{n+1}-p_{n}|\)

  4. \(|p-p_{n}|\leq\lambda^{n}\max\{p_{0}-a,b-p_{0}\}\)

Proof. We only show the proofs of the first two inequalities. Proofs of the other inequalities should be straightforward.

  1. By the triangle inequality property, we have

    \[\begin{equation*} |p-p_0| \le |p-p_1| + |p_1-p_0| \le \lambda |p-p_0| + |p_1-p_0|, \end{equation*}\]

    which leads to

    \[\begin{equation*} |p-p_0| \le \frac{|p_1-p_0|}{1-\lambda}. \end{equation*}\]

    Then we have from the proof of Theorem 10 that

    \[\begin{equation*} |p-p_n| \le \lambda^{n}|p-p_{0}| \le \frac{\lambda^{n}}{1-\lambda}|p_1-p_0|. \end{equation*}\]

  2. Similarly,

    \[\begin{equation*} |p-p_n| \le |p-p_{n+1}| + |p_{n+1}-p_n| \le \lambda |p-p_n| + |p_{n+1}-p_n|. \end{equation*}\]

    As a result, we have

    \[\begin{equation*} |p-p_n| \le \frac{|p_{n+1}-p_n|}{1-\lambda}. \end{equation*}\]

Excercise 2.6-1

Prove Corollary 3, part 4. (Hint: use mathematical induction and take the induction basis as \(n=0\).)

Geometric interpretation of fixed-point iteration

In Figure 4 and Figure 5, take a starting value \(p_0\) close to \(p\), and mark the first few fixed-point iterations, \(p_0,p_1,p_2\). Observe that the fixed-point iteration converges in the first graph, but diverges in the second one.

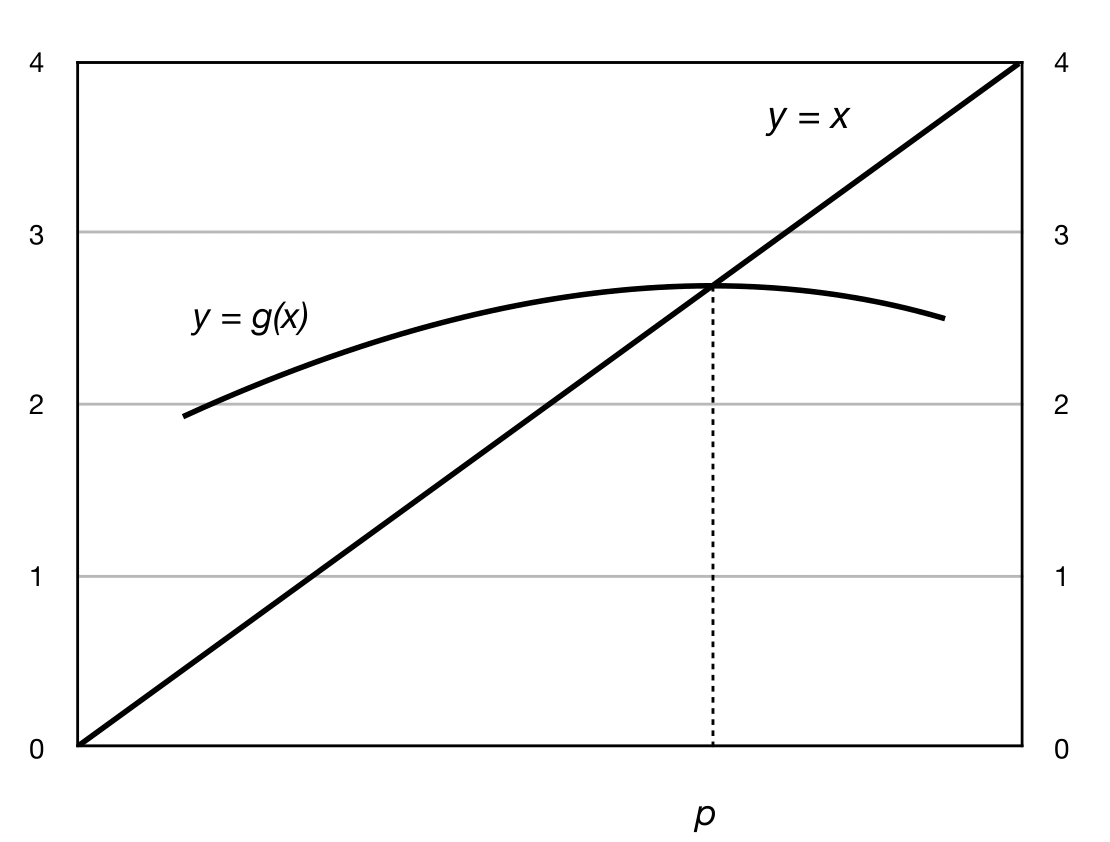
_images/fixedpt_conv.png

Fig. 4 Fixed-point iteration: \(|g'(p)|<1\).#

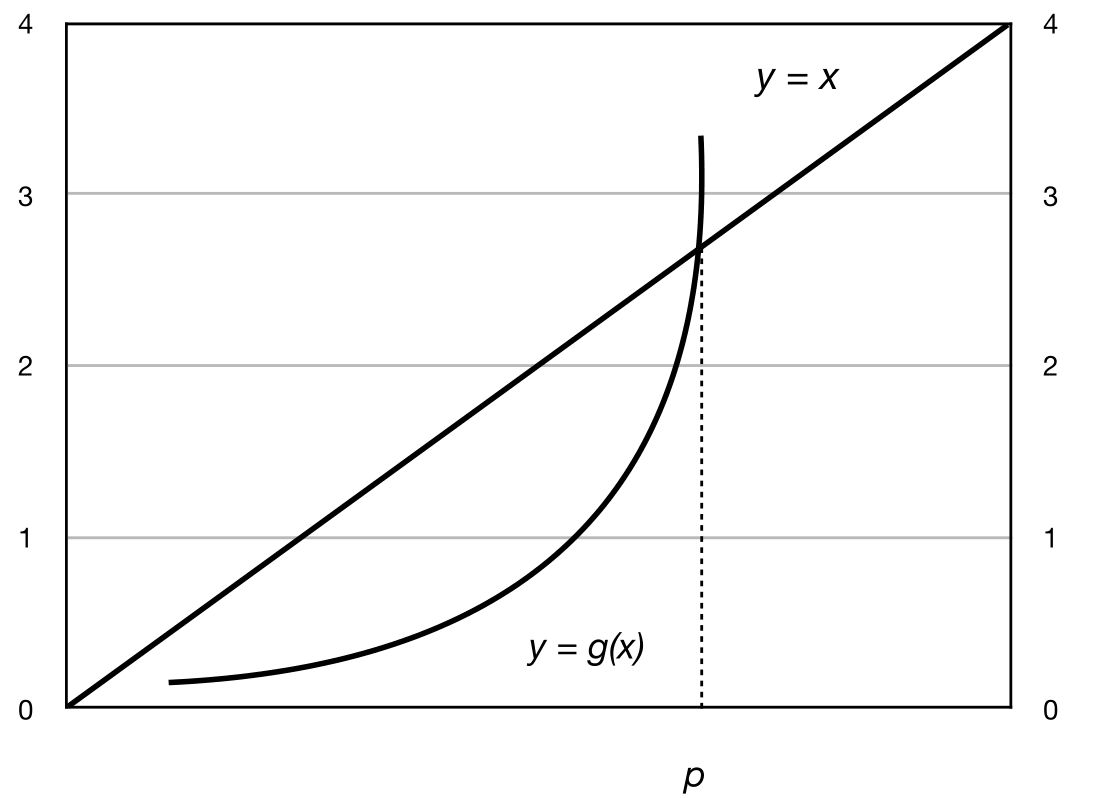
_images/fixedpt_div.png

Fig. 5 Fixed-point iteration: \(|g'(p)|>1\).#

Example 16

Consider the root-finding problem \(x^{3}-2x^{2}-1=0\) on \([1,3].\)

  1. Write the problem as a fixed-point problem, \(g(x)=x\), for some \(g\). Verify that the hypothesis of Theorem 10 (or Remark 7) is satisfied so that the fixed-point iteration converges.

  2. Let \(p_{0}=1.\) Use Corollary 3 to find \(n\) that ensures an estimate to \(p\) accurate to within \(10^{-4}\).

Solution

  1. There are several ways we can write this problem as \(g(x)=x:\)

    a. Let \(f(x)=x^{3}-2x^{2}-1\), and \(p\) be its root, that is, \(f(p)=0\). If we let \(g(x)=x-f(x)\), then \(g(p)=p-f(p)=p,\) so \(p\) is a fixed-point of \(g\). However, this choice for \(g\) will not be helpful, since \(g\) does not satisfy the first condition of Theorem 10: \(g(x)\notin[1,3]\) for all \(x\in[1,3]\) (\(g(3)=-5\notin[1,3]\)).

    b. Since \(p\) is a root for \(f\), we have \(p^3=2p^2+1\), or \(p=(2p^2+1)^{1/3}.\) Therefore, \(p\) is the solution to the fixed-point problem \(g(x)=x\) where \(g(x)=(2x^2+1)^{1/3}\).

    • \(g\) is increasing on \([1,3]\) and \(g(1)=1.44,g(3)=2.67\); thus \(g(x)\in[1,3]\) for all \(x\in[1,3]\). Therefore, \(g\) satisfies the first condition of Theorem 10.

    • \(g'(x)=\frac{4x}{3(2x^2+1)^{2/3}}\) and \(g'(1)=0.64,g'(3)=0.56\) and \(g'\) is decreasing on \([1,3]\). Therefore \(g\) satisfies the condition in Remark 7 with \(k=0.64\).

    Then, from Theorem 10 and Remark 7, the fixed-point iteration converges if \(g(x)=(2x^2+1)^{1/3}\).

  2. Take \(\lambda=k=0.64\) in Corollary 3 and use bound (4):

    \[\begin{equation*} |p-p_{n}|\leq(0.64)^{n}\max\{1-1,3-1\}=2(0.64^{n}). \end{equation*}\]

    We want \(2(0.64^{n})<10^{-4}\), which implies \(n\log0.64<-4\log10-\log 2\), or \(n>\frac{-4\log10-\log 2} {\log0.64}\approx22.19\). Therefore \(n=23\) is the smallest number of iterations that ensures an absolute error of \(10^{-4}\).

Python code for fixed-point iteration#

The following code starts with the initial guess \(p_0\) (pzero in the code), computes \(p_1=g(p_0)\), and checks if the stopping criterion \(|p_1-p_0|<\epsilon\) is satisfied. If it is satisfied the code terminates with the value \(p_1\). Otherwise \(p_1\) is set to \(p_0\), and the next iteration is computed.

import numpy as np
def fixedpt(g, pzero, eps, N):
    n = 1
    while n<N:
        print(n)
        pone = g(pzero)
        if np.abs(pone-pzero)<eps:
            print('p is ', pone, ' and the iteration number is ', n)
            return
        pzero = pone
        n += 1
    print('Did not converge. The last estimate is p = ', pzero)

Let’s find the fixed-point of \(g(x)=x\) where \(g(x)=(2x^2+1)^{1/3}\), with \(p_0=1\). We studied this problem in Example 16 where we found that 23 iterations guarantee an estimate accurate to within \(10^{-4}\). We set \(\epsilon=10^{-4}\), and \(N=30\), in the above code.

fixedpt(lambda x: (2*x**2+1)**(1/3), 1, 1e-4, 30)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
p is  2.205472095330031  and the iteration number is  19

The exact value of the fixed-point, equivalently the root of \(x^3-2x^2-1\), is 2.20556943. Then the exact error is:

2.205472095330031-2.20556943

-9.733466996930673e-05

A take home message and a word of caution:

  • The exact error, \(|p_n-p|\), is guaranteed to be less than \(10^{-4}\) after 23 iterations from Corollary 3, but as we observed in this example, this could happen before 23 iterations.

  • The stopping criterion used in the code is based on \(|p_n-p_{n-1}|\), not \(|p_n-p|\), so the iteration number that makes these quantities less than a tolerance \(\epsilon\) will not be the same in general.

Theorem 11

Assume \(p\) is a solution of \(g(x)=x\), and suppose \(g(x)\) is continuously differentiable in some interval about \(p\) with \(|g'(p)|<1\). Then the fixed-point iteration converges to \(p\), provided \(p_{0}\) is chosen sufficiently close to \(p\). Moreover, the convergence is linear if \(g'(p)\neq 0\).

Proof. Since \(g'\) is continuous and \(|g'(p)| < 1\), there exists an interval \(I=[p-\epsilon,p+\epsilon]\) such that \(|g'(x)|\leq k\) for all \(x\in I\), for some \(k<1\). Then, from Remark 6, we know \(|g(x)-g(y)|\leq k|x-y|\) for all \(x,y\in I\). Next, we argue that \(g(x)\in I\) if \(x\in I\). Indeed, if \(|x-p|<\epsilon,\) then

\[\begin{equation*} |g(x)-p|=|g(x)-g(p)|=|g'(\xi)||x-p|<k\epsilon<\epsilon \end{equation*}\]

hence \(g(x)\in I.\) Now use Theorem 10, setting \([a,b]\) to \([p-\epsilon,p+\epsilon]\), to conclude the fixed-point iteration converges.

To prove convergence is linear, we note

\[\begin{equation*} |p_{n+1}-p|=|g(p_n)-g(p)| = |g'(\xi_n)| |p_n-p| \leq k |p_n-p| \end{equation*}\]

which is the definition of linear convergence (with \(k\) being a positive constant less than 1).

We can actually prove something more:

\[\begin{equation*} \lim_{n\rightarrow\infty}\frac{|p_{n+1}-p|}{|p_{n}-p|} =\lim_{n\rightarrow\infty}\frac{|g(p_{n})-g(p)|}{|p_{n}-p|}=\lim_{n\rightarrow\infty}\frac{|g'(\xi_{n})||p_{n}-p|}{|p_{n}-p|} =\lim_{n\rightarrow\infty}|g'(\xi_{n})|=|g'(p)|. \end{equation*}\]

The last equality follows since \(g'\) is continuous, and \(\xi_{n}\rightarrow p\), which is a consequence of \(\xi_{n}\) being between \(p\) and \(p_{n}\), and \(p_{n}\rightarrow p\), as \(n\rightarrow\infty\).

Example 17

Let \(g(x)=x+c(x^{2}-2),\) which has the fixed-point \(p=\sqrt{2}\approx1.4142.\) Pick a value for \(c\) to ensure the convergence of fixed-point iteration. For the picked value \(c\), determine the interval of convergence \(I=[a,b],\) that is, the interval for which any \(p_{0}\) from the interval gives rise to a converging fixed-point iteration. Then write a Python code to test the results.

Solution.

Theorem 11 requires \(|g'(p)|<1.\) We have \(g'(x)=1+2xc,\) and thus \(g'(\sqrt{2})=1+2\sqrt{2}c\). Therefore

\[\begin{align*} |g'(\sqrt{2})| & <1\Rightarrow-1<1+2\sqrt{2}c<1\\ & \Rightarrow-2<2\sqrt{2}c<0\\ & \Rightarrow\frac{-1}{\sqrt{2}}<c<0. \end{align*}\]

Any \(c\) from this interval works: let’s pick \(c=-1/4\).

Now we need to find an interval \(I=[\sqrt{2}-\epsilon,\sqrt{2}+\epsilon]\) such that

\[\begin{equation*} |g'(x)|=|1+2xc|=\left|1-\frac{x}{2} \right| \leq k \end{equation*}\]

for some \(k<1,\) for all \(x\in I\). Plot \(g'(x)\) and observe that one choice is \(\epsilon=0.1\), so that \(I=[\sqrt{2}-0.1,\sqrt{2}+0.1]=[1.3142,1.5142]\). Since \(g'(x)\) is positive and decreasing on \(I=[1.3142,1.5142]\), \(|g'(x)|\leq1-\frac{1.3142}{2}=0.3429<1\), for any \(x\in I\). Then any starting value \(p_{0}\) from \(I\) gives convergence.

For \(c=-1/4\), the function becomes \(g(x)=x-\frac{x^2-2}{4}\). Pick \(p_0=1.5\) as the starting point. Using the fixed-point iteration code of the previous example, we obtain:

fixedpt(lambda x: x-(x**2-2)/4, 1.5, 1e-5, 15)

1
2
3
4
5
6
7
8
9
p is  1.414214788550556  and the iteration number is  9

The absolute error is:

1.414214788550556-(2**.5)

1.2261774609001463e-06

Let’s experiment with other starting values. Although \(p_0=2\) is not in the interval of convergence \(I\), we expect convergence since \(g'(2)=0\), and thus we can find another interval around \(p=\sqrt{2}\) that contains \(2\) such that \(g'(x)\) is bounded by a constant less than \(1\) on the interval.

fixedpt(lambda x: x-(x**2-2)/4, 2, 1e-5, 15)

1
2
3
4
5
6
7
8
9
10
p is  1.414214788550556  and the iteration number is  10

Let’s try \(p_0=-5\). Note that this is not only outside the interval of convergence \(I\), but \(g'(-5)=3.5>1\), so we do not expect convergence.

fixedpt(lambda x: x-(x**2-2)/4, -5, 1e-5, 15)

1
2
3
4
5
6
7
8
9
10
11

---------------------------------------------------------------------------
OverflowError                             Traceback (most recent call last)
Cell In[7], line 1
----> 1 fixedpt(lambda x: x-(x**2-2)/4, -5, 1e-5, 15)

Cell In[1], line 6, in fixedpt(g, pzero, eps, N)
      4 while n<N:
      5     print(n)
----> 6     pone = g(pzero)
      7     if np.abs(pone-pzero)<eps:
      8         print('p is ', pone, ' and the iteration number is ', n)

Cell In[7], line 1, in <lambda>(x)
----> 1 fixedpt(lambda x: x-(x**2-2)/4, -5, 1e-5, 15)

OverflowError: (34, 'Result too large')

Excercise 2.6-2

We want to find the root of \(f(x)=x-x^3\) by fixed-point iteration.

a. Show that a fixed-point of \(g(x)=x^{1/3}\) is a root of \(f(x)\). Then use Python and fixed-point iteration to find the fixed-point of \(g\). Run the code with \(p_0=1.1\) and \(p_0=0.9\) as the starting values. Does the fixed-point iteration converge to the fixed-point of the function? Is this expected from the convergence theorem for fixed-point iteration?

b. Show that a fixed-point of \(g(x)=x^3\) is a root of \(f(x)\). Then use Python and fixed-point iteration to find the fixed-point of \(g\). Run the code with \(p_0=1.1\) and \(p_0=0.9\) as the starting values. Does the fixed-point iteration converge to the fixed-point of the function? Is this expected from the convergence theorem for fixed-point iteration?

Let’s verify the linear convergence of the fixed-point iteration numerically in this example. We write another version of the fixed-pointcode, fixedpt2, and we compute \(\frac{p_n-\sqrt{2}}{p_{n-1}-\sqrt{2}}\) for each \(n\).

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

def fixedpt2(g, pzero, eps, N):
    n = 1
    arr = np.array([])
    error = 1.
    while n<N and error>eps:
        pone = g(pzero)
        error = np.abs(pone-pzero)
        arr = np.append(arr, (pone-2**0.5)/(pzero-2**0.5))
        pzero = pone
        n += 1
    return arr

arr = fixedpt2(lambda x: x-(x**2-2)/4, 1.5, 1e-7, 15)
arr

array([0.27144661, 0.28707161, 0.291222  , 0.29240652, 0.29275091,
       0.29285156, 0.29288102, 0.29288965, 0.29289217, 0.29289291,
       0.29289313, 0.29289319])

plt.plot(arr);
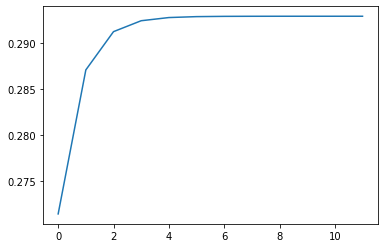
_images/891d29749266276ac3705109d8165f108cabc5f0735c3a733c96d419ea1ba929.png

The graph suggests the limit of \(\frac{p_n-\sqrt{2}}{p_{n-1}-\sqrt{2}}\) exists and it is around 0.295, supporting linear convergence.

Excercise 2.6-3

Let \(g\) be a differentiable function with a fixed point \(p\). Suppose \(|g'(x)|>1\) for all \(x\in I\), where \(I\) is an interval that contains \(p\). Show that the fixed-point iteration does not converge if \(p_0 \in I\) and \(p_0 \neq p\). (Hint: Prove that \(|p_1-p|>|p_0-p|\), \(|p_2-p|>|p_1-p|\), and so on, which means the iterates are going farther away from \(p\), as long as they are in the interval \(I\).)