4.1 Polynomial interpolation

In polynomial interpolation, we pick polynomials as the family of functions in the interpolation problem.

• Data: \((x_{i},y_{i}),i=0,1,...,n\)

• Family: Polynomials

The space of polynomials up to degree \(n\) is a vector space. We will consider three choices for the basis for this vector space:

• Basis:

  • Monomial basis: \(\phi_{k}(x)=x^{k}\)

  • Lagrange basis: \(\phi_{k}(x)=\prod_{j=0,j\neq k}^{n}\left(\frac{x-x_{j}}{x_{k}-x_{j}}\right)\)

  • Newton basis: \(\phi_{k}(x)=\prod_{j=0}^{k-1}(x-x_{j})\) where \(k=0,1,...,n\).

Once we decide on the basis, the interpolating polynomial can be written as a linear combination of the basis functions:

\[\begin{equation*} p_{n}(x)=\sum_{k=0}^{n}a_{k}\phi_{k}(x) \end{equation*}\]

where \(p_{n}(x_{i})=y_{i},i=0,1,...,n.\)

Here is an important question. How do we know that \(p_{n}\), a polynomial of degree at most \(n\) passing through the data points, actually exists? Or, equivalently, how do we know the system of equations \(p_{n}(x_{i})=y_{i},i=0,1,...,n\), has a solution?

The answer is given by the following theorem, which we will prove later in this section.

Theorem 20

If points \(x_{0},x_{1},...,x_{n}\) are distinct, then for real values \(y_{0},y_{1},...,y_{n},\) there is a unique polynomial \(p_{n}\) of degree at most \(n\) such that \(p_{n}(x_{i})=y_{i},i=0,1,...,n.\)

We mentioned three families of basis functions for polynomials. The choice of a family of basis functions affects:

• The accuracy of the numerical methods to solve the system of linear equations \(Aa=y\).

• The ease at which the resulting polynomial can be evaluated, differentiated, integrated, etc.

Monomial form of polynomial interpolation

Given data \((x_{i},y_{i}),i=0,1,...,n\), we know from the previous theorem that there exists a polynomial \(p_n(x)\) of degree at most \(n\), that passes through the data points. To represent \(p_n(x)\), we will use the monomial basis functions, \(1,x,x^{2},...,x^{n}\), or written more succinctly,

\[\begin{equation*} \phi_{k}(x)=x^{k},k=0,1,...,n. \end{equation*}\]

The interpolating polynomial \(p_n(x)\) can be written as a linear combination of these basis functions as

\[\begin{equation*} p_{n}(x)=a_{0}+a_{1}x+a_{2}x^{2}+...+a_{n}x^{n}. \end{equation*}\]

We will determine \(a_{i}\) using the fact that \(p_n\) is an interpolant for the data:

\[\begin{equation*} p_{n}(x_{i})=a_{0}+a_{1}x_{i}+a_{2}x_{i}^{2}+...+a_{n}x_{i}^{n}=y_{i} \end{equation*}\]

for \(i=0,1,...,n.\) Or, in matrix form, we want to solve

\[\begin{equation*} \underbrace{\begin{bmatrix}1 & x_{0} & x_{0}^{2} & ... & x_{0}^{n}\\ 1 & x_{1} & x_{1}^{2} & \cdots & x_{1}^{n}\\ \vdots & \vdots & \vdots & \vdots & \vdots\\ 1 & x_{n} & x_{n}^{2} & \cdots & x_{n}^{n} \end{bmatrix}}_A \underbrace{\begin{bmatrix}a_{0}\\ a_{1}\\ \vdots\\ a_{n} \end{bmatrix}}_a=\underbrace{\begin{bmatrix}y_{0}\\ y_{1}\\ \vdots\\ y_{n} \end{bmatrix}}_y \end{equation*}\]

for \([a_{0},...,a_{n}]^{T}\) where \([\cdot]^T\) stands for the transpose of the vector. The coefficient matrix \(A\) is known as the van der Monde matrix. This is usually an ill-conditioned matrix, which means solving the system of equations could result in large error in the coefficients \(a_{i}.\) An intuitive way to understand the ill-conditioning is to plot several basis monomials, and note how less distinguishable they are as the degree increases, making the columns of the matrix nearly linearly dependent.

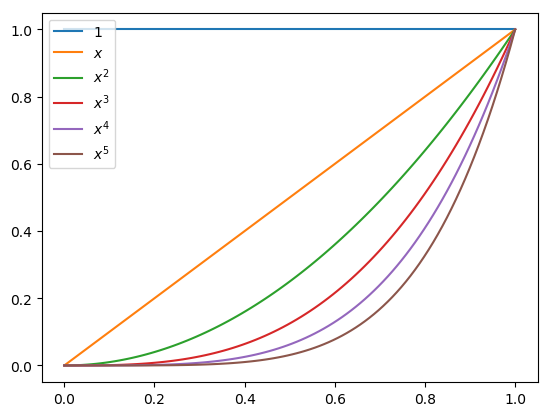
Fig. 6 Monomial basis functions

Solving the matrix equation \(Aa=b\) could also be expensive. Using Gaussian elimination to solve the matrix equation for a general matrix \(A\) requires \(O(n^3)\) operations. This means the number of operations grows like \(Cn^3\), where \(C\) is a positive constant1. However, there are some advantages to the monomial form: evaluating the polynomial is very efficient using Horner’s method, which is the nested form discussed in Exercises 1.3-4, 1.3-5 of Chapter 1, requiring \(O(n)\) operations. Differentiation and integration are also relatively efficient.

Lagrange form of polynomial interpolation

The ill-conditioning of the van der Monde matrix, as well as the high complexity of solving the resulting matrix equation in the monomial form of polynomial interpolation, motivate us to explore other basis functions for polynomials. As before, we start with data \((x_{i},y_{i}),i=0,1,...,n\), and call our interpolating polynomial of degree at most \(n\), \(p_n(x)\). The Lagrange basis functions up to degree \(n\) (also called cardinal polynomials) are defined as

\[\begin{equation*} l_{k}(x)=\prod_{j=0,j\neq k}^{n}\left(\frac{x-x_{j}}{x_{k}-x_{j}}\right),k=0,1,...,n. \end{equation*}\]

We write the interpolating polynomial \(p_n(x)\) as a linear combination of these basis functions as

\[\begin{equation*} p_{n}(x)=a_{0}l_{0}(x)+a_{1}l_{1}(x)+\cdots+a_{n}l_{n}(x). \end{equation*}\]

We will determine \(a_{i}\) from

\[\begin{equation*} p_{n}(x_{i})=a_{0}l_{0}(x_{i})+a_{1}l_{1}(x_{i})+\cdots+a_{n}l_{n}(x_{i})=y_{i} \end{equation*}\]

for \(i=0,1,\dots,n.\) Or, in matrix form, we want to solve

\[\begin{equation*} \underbrace{\begin{bmatrix}l_{0}(x_{0}) & l_{1}(x_{0}) & \cdots & l_{n}(x_{0})\\ l_{0}(x_{1}) & l_{1}(x_{1}) & \cdots & l_{n}(x_{1})\\ \vdots & \vdots & \vdots & \vdots\\ l_{0}(x_{n}) & l_{1}(x_{n}) & \cdots & l_{n}(x_{n}) \end{bmatrix}}_A \underbrace{\begin{bmatrix}a_{0}\\ a_{1}\\ \vdots \\ a_{n} \end{bmatrix}}_a=\underbrace{\begin{bmatrix}y_{0}\\ y_{1}\\ \vdots\\ y_{n} \end{bmatrix}}_y \end{equation*}\]

for \([a_{0},\dots,a_{n}]^{T}.\)

Solving this matrix equation is trivial for the following reason. Observe that \(l_{k}(x_{k})=1\) and \(l_{k}(x_{i})=0\) for all \(i\neq k.\) Then the coefficient matrix \(A\) becomes the identity matrix, and

\[\begin{equation*} a_{k}=y_{k}\text{ for }k=0,1,\dots,n. \end{equation*}\]

The interpolating polynomial becomes

\[\begin{equation*} p_{n}(x)=y_{0}l_{0}(x)+y_{1}l_{1}(x)+\cdots+y_{n}l_{n}(x). \end{equation*}\]

The main advantage of the Lagrange form of interpolation is that finding the interpolating polynomial is trivial: there is no need to solve a matrix equation. However, the evaluation, differentiation, and integration of the Lagrange form of a polynomial is more expensive than, for example, the monomial form.

Example 33

Find the interpolating polynomial using the monomial basis and Lagrange basis functions for the data: \((-1,-6),(1,0),(2,6).\)

Solution.

• Monomial basis: \(p_{2}(x)=a_{0}+a_{1}x+a_{2}x^{2}\)

\[\begin{equation*} \underbrace{\left[\begin{array}{ccc} 1 & x_{0} & x_{0}^{2}\\ 1 & x_{1} & x_{1}^{2}\\ 1 & x_{2} & x_{2}^{2} \end{array}\right]}_A \underbrace{\begin{bmatrix}a_{0}\\ a_{1}\\ a_{2} \end{bmatrix}}_a=\underbrace{\begin{bmatrix}y_{0}\\ y_{1}\\ y_{2} \end{bmatrix}}_y\Rightarrow\left[\begin{array}{ccc} 1 & -1 & 1\\ 1 & 1 & 1\\ 1 & 2 & 4 \end{array}\right]\begin{bmatrix}a_{0}\\ a_{1}\\ a_{2} \end{bmatrix}=\begin{bmatrix}-6\\ 0\\ 6 \end{bmatrix} \end{equation*}\]

We can use Gaussian elimination to solve this matrix equation, or get help from Python:

import numpy as np

A = np.array([[1,-1,1], [1,1,1], [1,2,4]])
A

array([[ 1, -1,  1],
       [ 1,  1,  1],
       [ 1,  2,  4]])

y = np.array([-6, 0, 6])
y

array([-6,  0,  6])

np.linalg.solve(A, y)

array([-4.,  3.,  1.])

Since the solution is \(a=[-4,3,1]^{T},\) we obtain

\[\begin{equation*} p_{2}(x)=-4+3x+x^{2}. \end{equation*}\]

• Lagrange basis: \(p_{2}(x) =y_{0}l_{0}(x)+y_{1}l_{1}(x)+y_{2}l_{2}(x)=-6l_{0}(x)+0l_{1}(x)+6l_{2}(x)\)

where

\[\begin{align*} l_{0}(x) & =\frac{(x-x_{1})(x-x_{2})}{(x_{0}-x_{1})(x_{0}-x_{2})}=\frac{(x-1)(x-2)}{(-1-1)(-1-2)}=\frac{(x-1)(x-2)}{6}\\ l_{2}(x) & =\frac{(x-x_{0})(x-x_{1})}{(x_{2}-x_{0})(x_{2}-x_{1})}=\frac{(x+1)(x-1)}{(2+1)(2-1)}=\frac{(x+1)(x-1)}{3} \end{align*}\]

therefore

\[\begin{align*} p_{2}(x) & =-6 \frac{(x-1)(x-2)}{6} +6 \frac{(x+1)(x-1)}{3}=-(x-1)(x-2)+2(x+1)(x-1). \end{align*}\]

If we multiply out and collect the like terms, we obtain \(p_2(x)=-4+3x+x^{2}\), which is the polynomial we obtained from the monomial basis earlier.

Exercise 4.1-1

Prove that \(\sum_{k=0}^{n}l_{k}(x)=1\) for all \(x,\) where \(l_{k}\) are the Lagrange basis functions for \(n+1\) data points. (Hint. First verify the identity for \(n=1\) algebraically, for any two data points. For the general case, think about what special function’s interpolating polynomial in Lagrange form is \(\sum_{k=0}^{n}l_{k}(x)\).)

Newton’s form of polynomial interpolation

The Newton basis functions up to degree \(n\) are

\[\begin{equation*} \pi_{k}(x)=\prod_{j=0}^{k-1}(x-x_{j}), k=0,1,\dots,n \end{equation*}\]

where \(\pi_{0}(x)=\prod_{j=0}^{-1}(x-x_{j})\) is interpreted as 1. The interpolating polynomial \(p_n\), written as a linear combination of Newton basis functions, is

\[\begin{align*} p_{n}(x) & =a_{0}\pi_{0}(x)+a_{1}\pi_{1}(x)+\cdots+a_{n}\pi_{n}(x)\\ & =a_{0}+a_{1}(x-x_{0})+a_{2}(x-x_{0})(x-x_{1})+\cdots+a_{n}(x-x_{0})\cdots(x-x_{n-1}). \end{align*}\]

We will determine \(a_{i}\) from

\[\begin{equation*} p_{n}(x_{i})=a_{0}+a_{1}(x_{i}-x_{0})+\cdots+a_{n}(x_i-x_{0})\cdots(x_i-x_{n-1})=y_{i}, \end{equation*}\]

for \(i=0,1,\dots,n,\) or in matrix form

\[\begin{equation*} \underbrace{\begin{bmatrix}1 & 0 & 0 & \ldots & 0\\ 1 & (x_{1}-x_{0}) & 0 & \ldots & 0\\ 1 & (x_{2}-x_{0}) & (x_{2}-x_{0})(x_{2}-x_{1}) & \ldots & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots\\ 1 & (x_{n}-x_{0}) & (x_{n}-x_{0})(x_{n}-x_{1}) & \ldots & \prod_{i=0}^{n-1}(x_{n}-x_{i}) \end{bmatrix}}_A \underbrace{\begin{bmatrix}a_{0}\\ a_{1}\\ \vdots\\ a_{n} \end{bmatrix}}_a=\underbrace{\begin{bmatrix}y_{0}\\ y_{1}\\ \vdots\\ y_{n} \end{bmatrix}}_y. \end{equation*}\]

Note that the coefficient matrix \(A\) is lower-triangular, and \(a\) can be solved by forward substitution, which is shown in the next example, in \(O(n^2)\) operations.

Example 34

Find the interpolating polynomial using Newton’s basis for the data: \((-1,-6),(1,0),(2,6)\).

Solution.

We have \(p_{2}(x)=a_{0}+a_{1}\pi_{1}(x)+a_{2}\pi_{2}(x)=a_{0}+a_{1}(x+1)+a_{2}(x+1)(x-1).\) Find \(a_{0},a_{1},a_{2}\) from

\[\begin{align*} p_2(-1)=-6 &\Rightarrow a_0+a_1(-1+1)+a_2(-1+1)(-1-1)=a_0=-6\\ p_2(1)=0 &\Rightarrow a_0+a_1(1+1)+a_2(1+1)(1-1)=a_0+2a_1=0\\ p_2(2)=6 &\Rightarrow a_0+a_1(2+1)+a_2(2+1)(2-1)=a_0+3a_1+3a_2=6 \end{align*}\]

or, in matrix form

\[\begin{equation*} \begin{bmatrix}1 & 0 & 0\\ 1 & 2 & 0\\ 1 & 3 & 3 \end{bmatrix}\begin{bmatrix}a_{0}\\ a_{1}\\ a_{2} \end{bmatrix}=\begin{bmatrix}-6\\ 0\\ 6 \end{bmatrix}. \end{equation*}\]

Forward substitution is:

\[\begin{gather*} a_{0}=-6\\ a_{0}+2a_{1}=0\Rightarrow-6+2a_{1}=0\Rightarrow a_{1}=3\\ a_{0}+3a_{1}+3a_{2}=6\Rightarrow-6+9+3a_{2}=6\Rightarrow a_{2}=1. \end{gather*}\]

Therefore \(a=[-6,3,1]^{T}\) and

\[\begin{equation*} p_{2}(x)=-6+3(x+1)+(x+1)(x-1). \end{equation*}\]

Multiplying out and simplifying give \(p_2(x)=-4+3x+x^2\), which is the polynomial discussed in Example 33.

Summary: The interpolating polynomial \(p_2(x)\) for the data, \((-1,-6),(1,0),(2,6)\), represented in three different basis functions is:

\[\begin{align*} \text{Monomial: } p_{2}(x) & = -4+3x+x^{2}\\ \text{Lagrange: } p_{2}(x)= & -(x-1)(x-2)+2(x+1)(x-1)\\ \text{Newton: } p_{2}(x)= & -6+3(x+1)+(x+1)(x-1) \end{align*}\]

Similar to the monomial form, a polynomial written in Newton’s form can be evaluated using the Horner’s method which has \(O(n)\) complexity:

\[\begin{align*} p_{n}(x)&=a_{0}+a_{1}(x-x_{0})+a_{2}(x-x_{0})(x-x_{1})+\cdots+a_{n}(x-x_{0})(x-x_{1})\cdots(x-x_{n-1})\\ &=a_{0}+(x-x_{0})(a_{1}+(x-x_{1})(a_{2}+\cdots+(x-x_{n-2})(a_{n-1}+(x-x_{n-1})(a_{n}))\cdots)) \end{align*}\]

Example 35

Write \(p_{2}(x)=-6+3(x+1)+(x+1)(x-1)\) using the nested form.

Solution.

\(-6+3(x+1)+(x+1)(x-1)=-6+(x+1)(2+x);\) note that the left-hand side has 2 multiplications, and the right-hand side has 1.

Complexity of the three forms of polynomial interpolation: The number of operations required in solving the corresponding matrix equation in each polynomial basis is:

• Monomial \(\rightarrow O(n^3)\)

• Lagrange \(\rightarrow\) trivial

• Newton \(\rightarrow O(n^2)\)

Evaluating the polynomials can be done efficiently using Horner’s method for monomial and Newton forms. A modified version of Lagrange form can also be evaluated using Horner’s method, but we do not discuss it here.

Exercise 4.1-2

Compute, by hand, the interpolating polynomial to the data \((-1,0)\), \((0.5,1)\), \((1,0)\) using the monomial, Lagrange, and Newton basis functions. Verify the three polynomials are identical.

It’s time to discuss some theoretical results for polynomial interpolation. Let’s start with proving Theorem 20 which we stated earlier:

Theorem 21

If points \(x_{0},x_{1},\dots,x_{n}\) are distinct, then for real values \(y_{0},y_{1},\dots,y_{n},\) there is a unique polynomial \(p_{n}\) of degree at most \(n\) such that \(p_{n}(x_{i})=y_{i},i=0,1,\dots,n.\)

Proof. We have already established the existence of \(p_{n}\) without mentioning it! The Lagrange form of the interpolating polynomial constructs \(p_{n}\) directly:

\[\begin{equation*} p_{n}(x)=\sum_{k=0}^{n}y_{k}l_{k}(x)=\sum_{k=0}^{n}y_{k}\prod_{j=0,j\neq k}^{n}\frac{x-x_{j}}{x_{k}-x_{j}}. \end{equation*}\]

Let’s prove uniqueness. Assume \(p_{n},q_{n}\) are two distinct polynomials satisfying the conclusion. Then \(p_{n}-q_{n}\) is a polynomial of degree at most \(n\) such that \((p_{n}-q_{n})(x_{i})=0\) for \(i=0,1,\dots,n.\) This means the non-zero polynomial \((p_{n}-q_{n})\) of degree at most \(n,\) has \((n+1)\) distinct roots, which is a contradiction.

The following theorem, which we state without proof, establishes the error of polynomial interpolation. Notice the similarities between this and Taylor’s Theorem 5.

Theorem 22

Let \(x_{0},x_{1},\dots,x_{n}\) be distinct numbers in the interval \([a,b]\) and \(f\in C^{n+1}[a,b].\) Then for each \(x\in[a,b],\) there is a number \(\xi\) between \(x_{0},x_{1},\dots,x_{n}\) such that

\[\begin{equation*} f(x)-p_{n}(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_{0})(x-x_{1})\cdots(x-x_{n}). \end{equation*}\]

The following lemma is useful in finding upper bounds for \(|f(x)-p_{n}(x)|\) using Theorem 22, when the nodes \(x_0,\dots,x_n\) are equally spaced.

Lemma 2

Consider the partition of \([a,b]\) as \(x_0=a,x_1=a+h,\dots,x_n=a+nh=b\). More succinctly, \(x_{i}=a+ih\) for \(i=0,1,\dots,n\) and \(h=\frac{b-a}{n}.\) Then for any \(x\in[a,b]\)

\[\begin{equation*} \prod_{i=0}^{n}|x-x_{i}|\leq\frac{1}{4}h^{n+1}n! \end{equation*}\]

Proof. Since \(x\in[a,b]\), it falls into one of the subintervals: let \(x\in[x_{j},x_{j+1}].\) Consider the product \(|x-x_{j}||x-x_{j+1}|.\) Put \(s=|x-x_{j}|\) and \(t=|x-x_{j+1}|.\) The maximum of \(st\) given \(s+t=h,\) using calculus, can be found to be \(h^{2}/4,\) which is attained when \(x\) is the midpoint, and thus \(s=t=h/2\). Then

\[\begin{align*} \prod_{i=0}^{n}|x-x_{i}| & =|x-x_{0}|\cdots|x-x_{j-1}||x-x_{j}||x-x_{j+1}||x-x_{j+2}|\cdots|x-x_{n}|\\ & \leq|x-x_{0}|\cdots|x-x_{j-1}|\frac{h^{2}}{4}|x-x_{j+2}|\cdots|x-x_{n}|\\ & \leq|x_{j+1}-x_{0}|\cdots|x_{j+1}-x_{j-1}|\frac{h^{2}}{4}|x_{j}-x_{j+2}|\cdots|x_{j}-x_{n}|\\ & =(j+1)h\cdots2h\left(\frac{h^{2}}{4}\right)(2h)\cdots(n-j)h\\ & =h^{j}(j+1)!\frac{h^{2}}{4}(n-j)!h^{n-j-1}\\ & \leq h^{n+1}\frac{n!}{4}. \end{align*}\]

Example 36

Find an upper bound for the absolute error when \(f(x)=\cos x\) is approximated by its interpolating polynomial \(p_n(x)\) on \([0,\pi/2]\). For the interpolating polynomial, use 5 equally spaced nodes (\(n=4\)) in \([0,\pi/2]\), including the endpoints.

Solution.

From Theorem 22,

\[\begin{equation*} |f(x)-p_{4}(x)|=\frac{|f^{(5)}(\xi)|}{5!}|(x-x_{0})\cdots(x-x_{4})|. \end{equation*}\]

We have \(|f^{(5)}(\xi)|\leq1.\) The nodes are equally spaced with \(h=(\pi/2-0)/4=\pi/8.\) Then from the previous lemma,

\[\begin{equation*} |(x-x_{0})\cdots(x-x_{4})|\leq\frac{1}{4}\left(\frac{\pi}{8}\right)^{5}4! \end{equation*}\]

and therefore

\[\begin{equation*} |f(x)-p_{4}(x)|\leq\frac{1}{5!}\frac{1}{4}\left(\frac{\pi}{8}\right)^{5}4!=4.7\times10^{-4}. \end{equation*}\]

Exercise 4.1-3

Find an upper bound for the absolute error when \(f(x)=\ln x\) is approximated by an interpolating polynomial of degree five with six nodes equally spaced in the interval \([1,2]\).

We now revisit Newton’s form of interpolation, and learn an alternative method, known as divided differences, to compute the coefficients of the interpolating polynomial. This approach is numerically more stable than the forward substitution approach we used earlier. Let’s recall the interpolation problem.

• Data: \((x_{i},y_{i}),i=0,1,...,n\)

• Interpolant in Newton’s form:

\[\begin{equation*} p_{n}(x)=a_{0}+a_{1}(x-x_{0})+a_{2}(x-x_{0})(x-x_{1})+\cdots+a_{n}(x-x_{0})\cdots(x-x_{n-1}) \end{equation*}\]

Determine \(a_{i}\) from \(p_{n}(x_{i})=y_{i},i=0,1,\dots,n\).

Let’s think of the \(y\)-coordinates of the data, \(y_{i}\), as values of an unknown function \(f\) evaluated at \(x_i\), i.e., \(f(x_{i})=y_{i}.\) Substitute \(x=x_{0}\) in the interpolant to get:

\[\begin{equation*} a_{0}=f(x_{0}). \end{equation*}\]

Substitute \(x=x_{1}\) to get \(a_{0}+a_{1}(x_{1}-x_{0})=f(x_{1})\) or,

\[\begin{equation*} a_{1}=\frac{f(x_{1})-f(x_{0})}{x_{1}-x_{0}}. \end{equation*}\]

Substitute \(x=x_{2}\) to get, after some algebra

\[\begin{equation*} a_{2}=\frac{\frac{f(x_{2})-f(x_{0})}{x_{2}-x_{1}}-\frac{f(x_{1})-f(x_{0})}{x_{1}-x_{0}}\frac{x_{2}-x_{0}}{x_{2}-x_{1}}}{x_{2}-x_{0}} \end{equation*}\]

which can be further rewritten as

\[\begin{equation*} a_{2}=\frac{\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}-\frac{f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}{x_{2}-x_{0}}. \end{equation*}\]

Inspecting the formulas for \(a_{0},a_{1},a_{2}\) suggests the following simplified new notation called divided differences:

\[\begin{align*} a_{0} & =f(x_{0})=\textcolor{red}{f[x_{0}]}\longrightarrow\text{0th divided difference}\\ a_{1} & =\frac{f(x_{1})-f(x_{0})}{x_{1}-x_{0}}=\textcolor{red}{f[x_{0},x_{1}]}\longrightarrow\text{1st divided difference}\\ a_{2} & =\frac{\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}-\frac{f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}{x_{2}-x_{0}}=\frac{f[x_{1},x_{2}]-f[x_{0},x_{1}]}{x_{2}-x_{0}} =\textcolor{red}{f[x_{0},x_{1},x_{2}]}\longrightarrow\text{2nd divided difference } \end{align*}\]

And in general, \(a_{k}\) will be given by the \(k\)th divided difference:

\[\begin{equation*} a_{k}=\textcolor{red}{f[x_{0},x_{1},\dots,x_{k}]}. \end{equation*}\]

With this new notation, Newton’s interpolating polynomial can be written as

\[\begin{align*} p_{n}(x)&=f[x_{0}]+\sum_{k=1}^{n}f[x_{0},x_{1},\dots,x_{k}](x-x_{0})\cdots(x-x_{k-1})\\ &=f[x_{0}]+f[x_{0},x_{1}](x-x_{0})+f[x_{0},x_{1},x_{2}](x-x_{0})(x-x_{1})+\cdots\\ &+f[x_{0},x_{1},\dots,x_{n}](x-x_{0})(x-x_{1})\cdots(x-x_{n-1}). \end{align*}\]

Here is the formal definition of divided differences:

Definition 13

Given data \((x_{i},f(x_{i})),i=0,1,\dots,n,\) the divided differences are defined recursively as

\[\begin{align*} f[x_{0}] & =f(x_{0})\\ f[x_{0},x_{1},\dots,x_{k}] & =\frac{f[x_{1},\dots,x_{k}]-f[x_{0},\dots,x_{k-1}]}{x_{k}-x_{0}} \end{align*}\]

where \(k=1,\dots,n.\)

Example 37

Find the interpolating polynomial for the data \((-1,-6),(1,0),(2,6)\) using Newton’s form and divided differences.

Solution.

We want to compute

\[\begin{equation*} p_{2}(x)=f[x_{0}]+f[x_{0},x_{1}](x-x_{0})+f[x_{0},x_{1},x_{2}](x-x_{0})(x-x_{1}). \end{equation*}\]

Here are the divided differences:

\[\begin{equation*} \begin{array}{cccc} x & f[x] & \text{First divided difference} & \text{Second divided difference}\\ \hline x_{0}=-1 & f[x_{0}]=\color{blue}{-6} & & \\ & & f[x_{0},x_{1}]=\frac{f[x_{1}]-f[x_{0}]}{x_{1}-x_{0}}=\color{blue}{3} & \\ x_{1}=1 & f[x_{1}]=0 & & f[x_{0},x_{1},x_{2}]=\frac{f[x_{1},x_{2}]-f[x_{0},x_{1}]}{x_{2}-x_{0}}=\color{blue}{1}\\ & & f[x_{1},x_{2}]=\frac{f[x_{2}]-f[x_{1}]}{x_{2}-x_{1}}=6 & \\ x_{2}=2 & f[x_{2}]=6 & & \\ \hline \end{array} \end{equation*}\]

Therefore

\[\begin{equation*} p_{2}(x)=\textcolor{blue}{-6}+\textcolor{blue}{3}(x+1)+\textcolor{blue}{1}(x+1)(x-1), \end{equation*}\]

which is the same polynomial we had in Example 34.

Theorem 23

The ordering of the data in constructing divided differences is not important, that is, the divided difference \(f[x_{0},\dots,x_{k}]\) is invariant under all permutations of the arguments \(x_{0},\dots,x_{k}\).

Proof. Consider the data \((x_{0},y_{0}),(x_{1},y_{1}),\dots,(x_{k},y_{k})\) and let \(p_{k}(x)\) be its interpolating polynomial:

\[\begin{align*} p_{k}(x) & =f[x_{0}]+f[x_{0},x_{1}](x-x_{0})+f[x_{0},x_{1},x_{2}](x-x_{0})(x-x_{1})+\cdots\\ & +f[x_{0},\dots,x_{k}](x-x_{0})\cdots(x-x_{k-1}). \end{align*}\]

Now let’s consider a permutation of the \(x_{i};\) let’s label them as \(\tilde{x}_{0},\tilde{x}_{1},\dots,\tilde{x}_{k}.\) The interpolating polynomial for the permuted data does not change, since the data \(x_{0},x_{1},\dots,x_{k}\) (omitting the \(y\)-coordinates) is the same as \(\tilde{x}_{0},\tilde{x}_{1},\dots,\tilde{x}_{k}\), just in different order. Therefore

\[\begin{align*} p_{k}(x) & =f[\tilde{x}_{0}]+f[\tilde{x}_{0},\tilde{x}_{1}](x-\tilde{x}_{0})+f[\tilde{x}_{0},\tilde{x}_{1},\tilde{x}_{2}](x-\tilde{x}_{0})(x-\tilde{x}_{1})+\cdots \\ &+f[\tilde{x}_{0},\dots,\tilde{x}_{k}](x-\tilde{x}_{0})\cdots(x-\tilde{x}_{k-1}). \end{align*}\]

The coefficient of the polynomial \(p_{k}(x)\) for the highest degree \(x^{k}\) is \(f[x_{0},\dots,x_{k}]\) in the first equation, and \(f[\tilde{x}_{0},\dots,\tilde{x}_{k}]\) in the second. Therefore they must be equal to each other.

Exercise 4.1-4

Find the interpolating polynomial \(p_2(x)\) for the data \((1,0),(-1,-6),(2,6)\) using Newton’s form and divided differences.

a. Is the polynomial the same as the interpolating polynomial found in Example 37? Is this expected?

b. Are the second divided differences of the interpolating polynomial of Example 37 and \(p_2(x)\) the same? Is this expected?

Exercise 4.1-5

Consider the function \(f\) given in the following table.

\[\begin{equation*} \begin{array}{ccccc} x & 1 & 2 & 4 & 6\\ \hline f(x) & 2 & 3 & 5 & 9\\ \end{array} \end{equation*}\]

a) Construct a divided difference table for \(f\) by hand, and write the Newton form of the interpolating polynomial using the divided differences.

b) Assume you are given a new data point for the function: \(x=3,y=4.\) Find the new interpolating polynomial. (Hint: Think about how to update the interpolating polynomial you found in part (a).)

c) If you were working with the Lagrange form of the interpolating polynomial instead of the Newton form, and you were given an additional data point like in part (b), how easy would it be (compared to what you did in part (b)) to update your interpolating polynomial?

Example 38

Before the widespread availability of computers and mathematical software, the values of some often-used mathematical functions were disseminated to researchers and engineers via tables. The following table, taken from [Abramowitz and Stegun, 1991], displays some values of the gamma function, \(\Gamma(x)=\int_0^\infty t^{x-1} e^{-t}dt\).

\[\begin{equation*} \begin{array}{ccccc} x & 1.750 & 1.755 & 1.760 & 1.765\\ \hline \Gamma (x) & 0.91906 & 0.92021 & 0.92137 & 0.92256\\ \end{array} \end{equation*}\]

Use polynomial interpolation to estimate \(\Gamma(1.761)\).

Solution.

The divided differences, with five-digit rounding, are:

\[\begin{equation*} \begin{array}{cccccc} i & x_{i} & f[x_{i}] & f[x_{i},x_{i+1}] & f[x_{i-1},x_{i},x_{i+1}] & f[x_{0},x_{1},x_{2},x_{3}]\\ \hline 0 & 1.750 & \color{blue}{0.91906} & & & \\ & & & \color{blue}{0.23} & & \\ 1 & 1.755 & 0.92021 & & \color{blue}{0.2} & \\ & & & 0.232 & & \color{blue}{26.667}\\ 2 & 1.760 & 0.92137 & & 0.6 & \\ & & & 0.238& & \\ 3 & 1.765 & 0.92256 & & & \\ \hline \end{array} \end{equation*}\]

Here are various estimates for \(\Gamma(1.761)\) using interpolating polynomials of increasing degrees:

\[\begin{align*} p_{1}(x) &=\textcolor{blue}{f[x_{0}]}+\textcolor{blue}{f[x_{0},x_{1}]}(x-x_{0})\Rightarrow p_{1}(1.761)=\textcolor{blue}{0.91906+0.23}(1.761-1.750)=0.92159\\ p_{2}(x) &=f[x_{0}]+f[x_{0},x_{1}](x-x_{0})+\textcolor{blue}{f[x_{0},x_{1},x_{2}]}(x-x_{0})(x-x_{1})\\ &\Rightarrow p_{2}(1.761)=0.92159+\textcolor{blue}{(0.2)}(1.761-1.750)(1.761-1.755)=0.92160\\ p_{3}(x) & =p_{2}(x)+\textcolor{blue}{f[x_{0},x_{1},x_{2},x_{3}]}(x-x_{0})(x-x_{1})(x-x_{2})\\ &\Rightarrow p_{3}(1.761)=0.9216+\textcolor{blue}{26.667}(1.761-1.750)(1.761-1.755)(1.761-1.760)=0.92160. \end{align*}\]

Next we will change the ordering of the data and repeat the calculations. We will list the data in decreasing order of the \(x\)-coordinates:

\[\begin{equation*} \begin{array}{cccccc} i & x_{i} & f[x_{i}] & f[x_{i},x_{i+1}] & f[x_{i-1},x_{i},x_{i+1}] & f[x_{0},x_{1},x_{2},x_{3}]\\ \hline 0 & 1.765 & \color{blue}{0.92256} & & & \\ & & & \color{blue}{0.238} & & \\ 1 & 1.760 & 0.92137 & & \color{blue}{0.6} & \\ & & & 0.232 & & \color{blue}{26.667}\\ 2 & 1.755 & 0.92021 & & 0.2 & \\ & & & 0.23 & & \\ 3 & 1.750 & 0.91906 & & & \\ \hline \end{array} \end{equation*}\]

The polynomial evaluations are:

\[\begin{align*} p_{1}(1.761) & =\textcolor{blue}{0.92256}+\textcolor{blue}{0.238}(1.761-1.765)=0.92161\\ p_{2}(1.761) & =0.92161+\textcolor{blue}{0.6}(1.761-1.765)(1.761-1.760)=0.92161\\ p_{3}(1.761) & =0.92161+\textcolor{blue}{26.667}(1.761-1.765)(1.761-1.760)(1.761-1.755)=0.92161. \end{align*}\]

Summary of results:

The following table displays the results for each ordering of the data, together with the correct \(\Gamma(1.761)\) to 7 digits of accuracy.

\[\begin{equation*} \begin{array}{ccc} \hline \text{Ordering} & (1.75,1.755,1.76,1.765) & (1.765,1.76,1.755,1.75) \\ \hline p_{1}(1.761) & 0.92159 & 0.92161\\ p_{2}(1.761) & 0.92160 & 0.92161\\ p_{3}(1.761) & 0.92160 & 0.92161\\ \hline \Gamma(1.761) & \color{red}{0.9216103} & \color{red}{0.9216103}\\ \hline \end{array} \end{equation*}\]

Exercise 4.1-6

Answer the following questions:

a) Theorem 23 stated that the ordering of the data in divided differences does not matter. But we see differences in the two tables above. Is this a contradiction?

b) \(p_{1}(1.761)\) is a better approximation to \(\Gamma(1.761)\) in the second ordering. Is this expected?

c) \(p_{3}(1.761)\) is different in the two orderings; however, this difference is due to rounding error. In other words, if the calculations can be done exactly, \(p_{3}(1.761)\) will be the same in each ordering of the data. Why?

Exercise 4.1-7

Consider a function \(f(x)\) such that \(f(2)=1.5713\), \(f(3)=1.5719,f(5)=1.5738,\) and \(f(6)=1.5751.\) Estimate \(f(4)\) using a second degree interpolating polynomial (interpolating the first three data points) and a third degree interpolating polynomial (interpolating the first four data points). Round the final results to four decimal places. Is there any advantage here in using a third degree interpolating polynomial?

Python code for Newton interpolation

Consider the following divided difference table.

(26)\[\begin{split}\begin{array}{cccc} x & f(x) & f[x_{i},x_{i+1}] & f[x_{i-1},x_{i},x_{i+1}]\\ \hline x_{0} & \color{red}{y_{0}} & & \\ & & \color{red}{\frac{y_{1}-y_{0}}{x_{1}-x_{0}}=f[x_{0},x_{1}]} & \\ x_{1} & y_{1} & & \color{red}{\frac{f[x_{1},x_{2}]-f[x_{0},x_{1}]}{x_{2}-x_{0}}=f[x_0,x_1,x_2]}\\ & & \frac{y_{2}-y_{1}}{x_{2}-x_{1}}=f[x_{1},x_{2}] & \\ x_{2} & y_{2} & & \\ \hline \end{array}\end{split}\]

There are \(2+1=3\) divided differences in the table, not counting the 0th divided differences. In general, the number of divided differences to compute is \(1+\cdots+n=n(n+1)/2\). However, to construct Newton’s form of the interpolating polynomial, we need only \(n\) divided differences and the 0th divided difference \(y_0\). These numbers are displayed in red in Table (26). The important observation is, even though all the divided differences have to be computed in order to get the ones needed for Newton’s form, they do not have to be all stored. The following Python code is based on an efficient algorithm that goes through the divided difference calculations recursively, and stores an array of size \(m=n+1\) at any given time. In the final iteration, this array has the divided differences needed for Newton’s form.

Let’s explain the idea of the algorithm using the simple example of Table (26). The code creates an array \(a=(a_0,a_1,a_2)\) of size \(m=n+1\), which is three in our example, and sets

\[\begin{equation*} a_0=\textcolor{red}{y_0},a_1=y_1,a_2=y_2. \end{equation*}\]

In the first iteration (for loop, \(j=1\)), \(a_1\) and \(a_2\) are updated:

\[\begin{equation*} a_1:=\frac{a_1-a_0}{x_1-x_0}=\frac{y_1-y_0}{x_1-x_0}=\textcolor{red}{f[x_0,x_1]},a_2:=\frac{a_2-a_1}{x_2-x_1}=\frac{y_2-y_1}{x_2-x_1}. \end{equation*}\]

In the last iteration (for loop, \(j=2\)), only \(a_2\) is updated:

\[\begin{equation*} a_2:=\frac{a_2-a_1}{x_2-x_0}=\frac{ \frac{y_2-y_1}{x_2-x_1}-\frac{y_1-y_0}{x_1-x_0} }{x_2-x_0}=\textcolor{red}{f[x_0,x_1,x_2]}. \end{equation*}\]

The final array \(a\) is

\[\begin{equation*} a=(\color{red}{y_0,f[x_0,x_1],f[x_0,x_1,x_2]}) \end{equation*}\]

containing the divided differences needed to construct the Newton’s form of the polynomial.

Here is the Python function diff that computes the divided differences. The code uses a function we have not used before: np.flip(np.arange(j,m)). An example illustrates what it does the best:

import numpy as np

np.flip(np.arange(2,6))

array([5, 4, 3, 2])

In the code diff the inputs are the \(x\)- and \(y\)-coordinates of the data. The numbering of the indices starts at 0.

def diff(x, y):
    m = x.size # here m is the number of data points.
    # the degree of the polynomial is m-1
    a = np.zeros(m)
    for i in range(m):
        a[i] = y[i]
    for j in range(1, m):
        for i in np.flip(np.arange(j,m)):
            a[i] = (a[i]-a[i-1]) / (x[i]-x[i-(j)])
    return a

Let’s compute the divided differences of Example 37:

diff(np.array([-1,1,2]), np.array([-6,0,6]))

array([-6.,  3.,  1.])

These are the divided differences in the second ordering of the data in Example 38:

diff(np.array([1.765,1.760,1.755,1.750]),
     np.array([0.92256,0.92137,0.92021,0.91906]))

array([ 0.92256   ,  0.238     ,  0.6       , 26.66666667])

Now let’s write a code for the Newton form of polynomial interpolation. The inputs to the function newton are the \(x\)- and \(y\)-coordinates of the data, and where we want to evaluate the polynomial: \(z\). The code uses the divided differences function diff discussed earlier to compute:

\[\begin{equation*} f[x_{0}]+f[x_{0},x_{1}](z-x_{0})+\cdots +f[x_{0},x_{1},\dots,x_{n}](z-x_{0})(z-x_{1})\cdots(z-x_{n-1}) \end{equation*}\]

def newton(x, y, z):
    m = x.size # here m is the number of data points, not the degree
    # of the polynomial
    a = diff(x, y)
    sum = a[0]
    pr = 1.0
    for j in range(m-1):
        pr *= (z-x[j])
        sum += a[j+1]*pr
    return sum

Let’s verify the code by computing \(p_3(1.761)\) of Example 38:

newton(np.array([1.765,1.760,1.755,1.750]),
       np.array([0.92256,0.92137,0.92021,0.91906]), 1.761)

0.92160496

Exercise 4.1-8

This problem discusses inverse interpolation which gives another method to find the root of a function. Let \(f\) be a continuous function on \([a,b]\) with one root \(p\) in the interval. Also assume \(f\) has an inverse. Let \(x_{0},x_{1},\dots,x_{n}\) be \(n+1\) distinct numbers in \([a,b]\) with \(f(x_{i})=y_{i},i=0,1,\dots,n.\) Construct an interpolating polynomial \(P_{n}\) for \(f^{-1}(x),\) by taking your data points as \((y_{i},x_{i}),i=0,1,\dots,n.\) Observe that \(f^{-1}(0)=p,\) the root we are trying to find. Then, approximate the root \(p\), by evaluating the interpolating polynomial for \(f^{-1}\) at 0, i.e., \(P_{n}(0)\approx p.\) Using this method, and the following data, find an approximation to the solution of \(\log x=0.\)

\[\begin{equation*} \begin{array}{ccccc} x & 0.4 & 0.8 & 1.2 & 1.6\\ \hline \log x & -0.92 & -0.22 & 0.18 & 0.47\\ \end{array} \end{equation*}\]

AS91

M. Abramowitz and I.A. Stegun. Handbook of mathematical functions: with formulas, graphs, and mathematical tables. Volume 55. Courier Corporation, 1991.

---

1

The formal definition of the big O notation is as follows: we write \(f(n)=O(g(n))\) as \(n\rightarrow \infty\) if and only if there exists a positive constant \(M\) and a positive integer \(n^*\) such that \(|f(n)|\leq M g(n)\) for all \(n\geq n^*\).